Back

Gem Hunter

An artificial agent that attempts to solve a modified version of Minesweeper, where the goal is to figure out which cells contain gems, in addition to cells with mines hinted by cells containing numbers. A project for the Artificial Intelligence course.

Preface

Requirements and checklist:

No.	Criteria	Self Grading
1	Solution description: describe the correct logical principles for generating CNFs	`30/30`
2	Generate CNFs automatically	`10/10`
3	Use `pysat` to solve CNFs correctly	`10/10`
4	Implement an optimal algorithm to solve CNFs without a library	`10/10`
5	Program brute-force algorithm to compare with your chosen algorithm Program backtracking algorithm to compare with your chosen algorithm	`10/10`
6	Documents and other resources that you need to write and analysis in your report: Thoroughness in analysis and experimentation Give at least 5 test cases with different sizes (5x5, 9x9, 11x11, 15x15, 20x20…) to check your solution Comparing results and performance	`30/30`
	Total	`100/100`

Preliminiaries

Description

Gem Hunter is a variant of the classic game Minesweeper, with the caveat is that instead of just mines (or traps, in this variant), there are also gems to excavate.

This project aims to provide an agent, or a solver that solves this specific variant of Minesweeper. The solver shall take in a board, work out in its innards, and retrieve back a solution (where traps are, and where gems are).

Main collaborators:

Getting Started

There exists a file requirements.txt in the provided source files, that lists out what packages and modules were used, that can be installed by pip. But mainly, the true carriers of this project consist of:

python-sat for dealing with CNFs and automatic solvers. (We mistook it here, and thought pysat was it, but that module was for satellite data analysis)
mypy for static type-checking. Even though not everyone follows convention, it’s nice to have to point out inconsistencies in codes, to reduce frustrating difficult to understand runtime errors.
pandas and numpy were on standby. They were planned to be used for representing data in array-like structures, which provide a very straightforward way to manipulate as per array languages like Uiua, APL or J.

The data is represented as followed:

Any number greater than or equal to 0 denotes the number of traps around it in all 8 directions.
A number -1 denotes a trap, or a mine.
A number -2 denotes a gem.
A number -3 denotes an unknown cell (for example, when the board is inputted without any traps and gems revealed yet, and even though, this is not typically used as both -1 and -2 are treated as unknown cells in all algorithms).

The data returned shall be interpreted as followed:

The board is labelled by an index number, from left to right, from top to bottom (we’re not Japanese), starting with 1, up to (height * width).
The data returned is in a form of a list, where negatives denote a trap and positives denote a gem.
For example, the data [1, 2, -3, 4] would mean the first four cells are unknown, but after solving, it is decided that the first two cells, and the fourth cell all contain gems, and the third cell contains a trap.

Cogs of the System

No CEO is at their place today, without the minimum wage factory worker bending over. No system is complete without small, seemingly insignificant cogs spinning inside.

The demon lord has been terrorizing the world of Aionios since the dawn of time, now, it’s up to the renowned hero to rise up and liberate the lands. The legend tells that the secret to the demon lord’s weakness is hidden deep inside a dungeon, with many Gem Hunter puzzles. Since this campaign involves CNFs and solving such cases, we thought that from a Minesweeper provided board, from each cell shall yield a certain clause, then combining all with a conjunction would complete the aforementioned CNF. This proved to be difficult, as there are no discernible methods to generate a CNF from a cell, or a board as a whole.

That’s when @sytanl had the idea that, since it’s possible to generate DNFs (disjunctive normal forms, basically the opposite equivalence of CNFs) from each cell. For example, if a cell has 4 unknown cells around it, and it has the number 2, which means there can be $4\choose 2$ ways of mines can be in (each mine and each gem is the same, which is why this is a combination, and not a permutation).

Then using the DNFs provided, the hero @sytanl has found a way to convert a DNF formula into a CNF formula, which now is possible to be fed in the solvers of python-sat. Thus, the dungeon is already cleared on paper. The idea has been fortified. That idea is doable. The hero assembles his team of adventurers: the tank @xiao-honsu, the mage @hikawi, and the sand wall @khahhy as he embarks on the rainbow road to victory, only implementations are left.

Building the Omnitool

The party started to assemble machine parts, tools, and laptops to start working on a magic tool that is able to break down any Gem Hunter puzzle in the way.

Input/Output

To feed the puzzle into the tool, it needs an input and/or an output module, which allows it to then give back the solution after solving. This is done through the reader.py component of the tool, which reads in data in the format of:

2,_,2
2,_,_
1,1,1

Where _ denotes a cell that has yet to be solved, and numbers denote the number of traps around it. This component also provides a service to output the data back, in the format of, if it is solved:

2,T,2
2,T,G
1,1,1

Disjunctive Normal Forms

Given a board, it is not consistently possible to provide a CNF just out of nowhere, so the hero chose to apply a modulation on DNFs, that can return a CNF for him to work with.

Generating the DNF works as followed, given the board, and the cell at which the DNF should apply to:

If the cell has a number below 0, which means it’s considered an unknown cell. An unknown cell has no information to provide, so this returns an empty clause.
Retrieves all valid neighbors of the cell, which are cells that are not out of bounds, and are unknown cells.
Do a combination of run length equal to the value of the cell on its neighbors.

Conjunctive Normal Forms

Given a DNF clause, the hero applies an advanced level of magic to convert it to a CNF clause.

Initialize the CNF with an empty clause.
Iterate through each clause in the DNF.
Create a dictionary of new literals negated. Initialize an empty list to store next iteration’s CNF clauses.
Iterate through every clause of the current CNF, each new literal. If the literal negated is not in the clause, create a new clause with the literal added, and appending it to the new CNF list if the new clause is not a subset of any other existing clause in the new CNF.

Here, we’re already done. The hero let out an exhausted sigh. Feeding this into the blade of python-sat should take care of the rest of the work, and yields a result of where gems and traps are instantly.

Self-solve

The tank @xiao-honsu proposed a way of his own to forge a blade that can cut through the fabrics of the puzzle, instead of relying on an externally forged sword like python-sat. It effectively works like assigning variables in a CSP.

Clause Validator: check every clause, if there is one false clause then the model is false, return False. If all clauses make sense, then return the model itself. If the model does not have enough information, then return True (multiple solutions).
Clause Purifier: finds all pure symbols (or symbols that appear only once in the entire formula), assign a value to that symbol then recurse.
Clause Selection: finds a unit symbol, or symbols that only appear in the formula as a single clause by itself, assign a value to that symbol then recurse.
If neither works, pops a random symbol, assigns and recurses.

However, whether to compare the sharpness of the tank’s blade and the conventional weapon, it is up to the sand wall to check.

Sharpness Comparison

Note: there are chances of 50/50 in any Minesweeper games with a peculiar enough setup. For example, for this 2x2 board:

1 1
_ _

Then either of the unknown cell can be a mine, and the other can be a gem, and both are equally valid. This explains the discrepancy sometimes, between the cutting result of @xiao-honsu’s blade and the conventional blade of python-sat.

Results are as followed:

5x5: 5x5

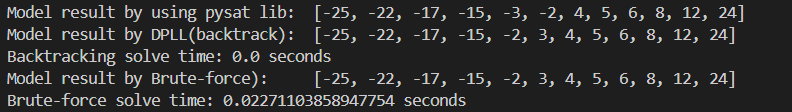
9x9: 9x9

11x11: 11x11

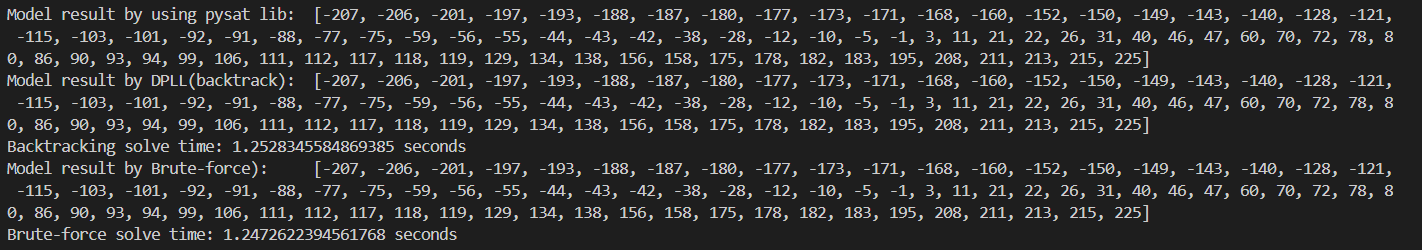
15x15: 15x15

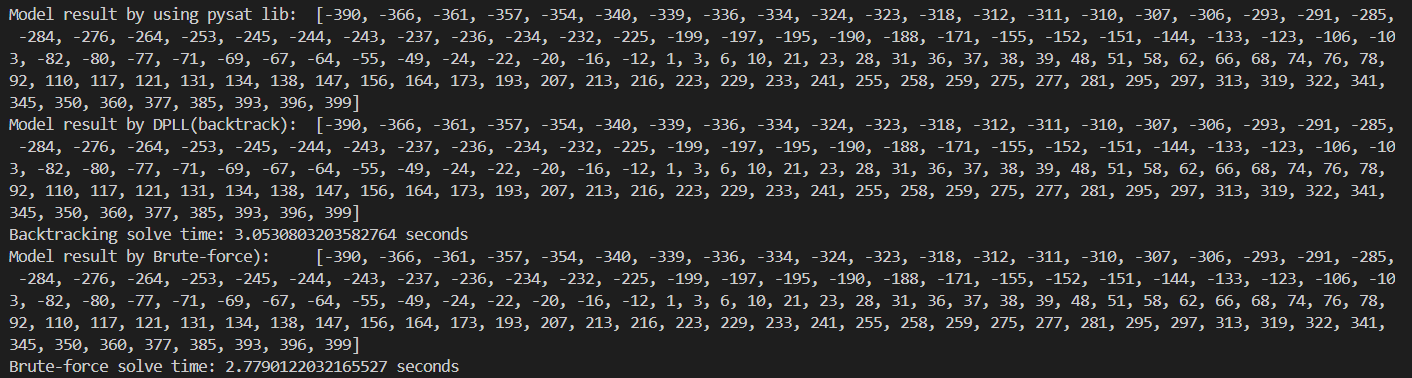
20x20: 20x20

If the above weaponsmithing data is a little bit too clustered and difficult to read, here it is in another way to represent:

Dimensions	Backtracking	Brute-force
5x5	0s	0.0227s
9x9	0.0068s	0s
11x11	0.0554s	0.057s
15x15	1.2528s	1.2473s
20x20	3.053s	2.77s

Unexpectedly, the data and time recorded doesn’t conform to any noticeable rules or patterns, where it’s kind of just all over the place, neck and neck against each other, and neither proved to be dominantly superior.

Seniors Grace

As anyone has expected, the hero did not go from rags to riches. We did not reinvent the wheel, and built on top of what is already available out there.