DSA Challenge - Bloom Filter

Features

Registering a new account, with checks for existing accounts using a Bloom Filter.
Logging in and out of an account.
Changing passwords of an existing account.
Registering multiple accounts at once, using credentials provided in a separate text file.

Research

Group Information

We split the work into corresponding 3 parts to do across 2 days (Wednesday 2/8/23 and Thursday 3/8/23):

One would do the Input-Output or IO part (including menus and files) of the programming section.
One would do the Core Mechanics (including the filter, applying constraints and providing functions for the IO one’s work) part of the programming section.
One would do the researches mainly and compile everything into one composition, which is this document. (Me)

Introduction

A Bloom filter is a probabilistic data structure, conceived by Burton Howard Bloom in 1970, that trades off error-freeness for space efficiency. It is mainly used to check membership of a certain element against a set. It is probabilistic, because there is a small probability of the check yielding a false positive, which means that it may return true, regardless of the element’s actual membership. However, false negatives are impossible. In other words, it is a special filter that when checking, it can yield a Definitely not there or a It’s there, maybe.

The high level view is that it is a surjective map from all elements of $x\in X$ , and maps to some $y \in Y$ via means of one, or multiple hash functions.

For simple Bloom filters, the distinction between a false positive and a true positive is impossible. It is mostly used to prevent unnecessary disk access. For practical example, Google Chrome previously used a Bloom filter to identify malicious URLs, and if the filter yields a positive result, will the browser warn the user, as if not, it is, definitely not malicious.

State the factors to estimate the optimal size of the bit array and the number of hash functions for a Bloom filter

At its very core, Bloom filters are a type of data structure that trades false positives for space efficiency for large data sets. So, the error rate (or the false positive rate) is a very important factor anywhere related to these filters. In addition to that, the number of elements we expect to add to the filter also plays an important role in how many slots we should allocate to the bitset. Summarized, the optimal size of the bit array depends mostly on the error rate and the number of elements.

The optimal number of bits per element is $-\frac{\log_2\epsilon}{\ln2}$ . Therefore, let $n$ be the number of elements we wish to insert, and $\epsilon$ be the error rate desired at $n$ elements, then the optimal size can be calculated with:

\frac{m}{n}=-\frac{\log_2\epsilon}{\ln2} \implies m = -\frac{n\log_2\epsilon}{\ln 2} = -n\cdot \frac{\ln\epsilon}{\ln2}\cdot \frac1{\ln2} = -\frac{n\ln\epsilon}{\ln^22}

The count of hashers, or hash functions is again, dependent on the number of elements we expect the filter to have at most, as a good set of hashers should uniformly distribute slots across the bitset. But too many hashers compared to the bitset size will prove to be redundant, and there will be more false positives, so it also has to depend on the number of bits. But, the number of bits itself also depends on the error rate. So, it still boils down to the error rate being the most important factor. Summarized, the optimal number of hashers depend on the number of elements and the number of bits.

With $m$ being the bitset size, and $n$ being the elements count, we can calculate the optimal number of hash functions:

k = \frac{m}{n}\ln2 = -\log_2\epsilon

How do hash functions impact the performance and accuracy of a Bloom filter?

As insertions and queries require going through a set of hash functions, both of these operations’ complexity would be $O(k)$ with $k$ being the number of hash functions. If one of these hash functions have a, for the lack of a better word, worse complexity, it would affect both of these operations heavily.

Also, the number of hashers also dictate how many bits get flipped during an insertion. If there are way too few hashers, queries would only check that many bits, the fewer bits checked, the higher rate of false positives. False positive rate can be derived with the following formula:

\epsilon = \left( 1 - \left[ 1 - \frac1m \right]^{kn} \right)^{k}

For the same exemplary $m$ and $n$ (with $n$ being substantially smaller than $m$ ) of some arbitrarily large numbers, as $k$ tends downwards, false positive rates go up:

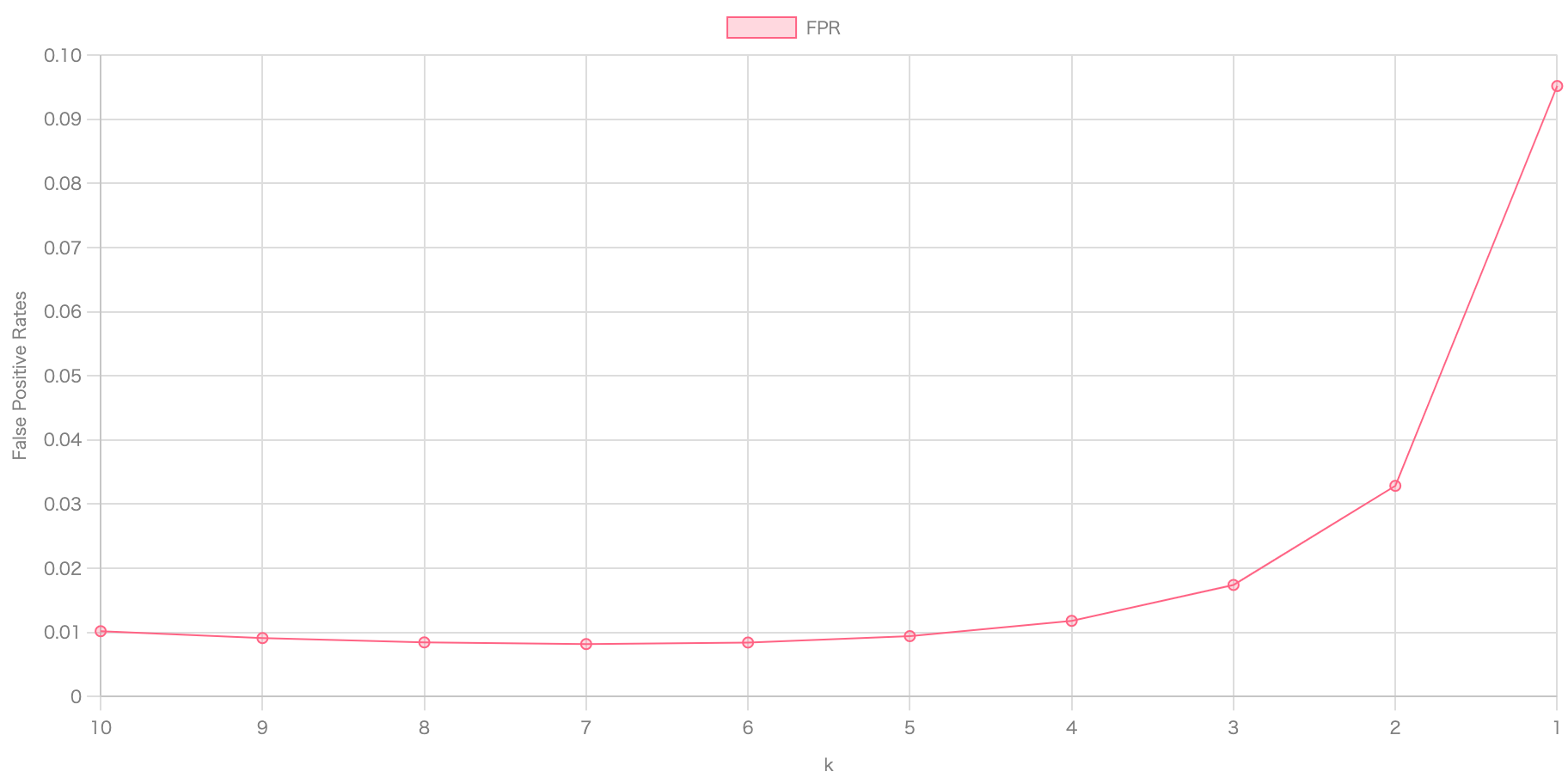
Graph

There is also a slight descend as with $m=10k$ and $n=1k$ , $k = 10$ is not the optimal number of hash functions, yet. But it starts spiking up real fast as $k$ trends towards 1.

Do lookup operations on Bloom filter always give correct results? If not, indicate the estimation method for false positive rate.

No, lookup operations on Bloom filters will have a chance of turning up a false positive, after all, it is a data structure that favors probability over error-freeness, otherwise, we would have gone with similarly purposed structures like hash tables.

Assume, $m$ is the number of bits in the array, the probability that after a hash, one bit gets flipped to 1 is $\frac1m$ . So, after a hash, the probability that one bit hasn’t been flipped to 1 is $P(0)=(1-\frac1m)^k$ with $k$ being the number of hashers.

After inserting $n$ elements, the probability that one bit is still 0 is $P(0)^n$ , and then, the probability that it is already $1$ is therefore: $P(1)=1-P(0)^n$ . If we wants to query for an element, the query goes through $k$ number of hash functions, then if they are all $1$ , it would return a Maybe there claim, as the probability of that happening is now $P(1)^k$ . This is the false positive rate, with formula written in full as:

\epsilon = P(1)^k = (1 - P(0)^n)^k= \left[1-\left(1-\frac1m\right)^{kn}\right]^k

The same as what we used in the previous section.

Does the insertion of elements affect the false positive rate in a Bloom filter?

Yes, as the Bloom filter fills up with $1$ , false positive rates is obviously going to go up. If at some point, the Bloom filter only is comprised of $1$ s, any queries would yield a Maybe there.

This is why we usually want to estimate how many elements we would like in a Bloom filter, and the false positive rate to go with it. At the specific number of $n$ , $\epsilon$ would be our desired rate. Going over $n$ , $\epsilon$ naturally goes up. If still much less than $n$ , $\epsilon$ hasn’t reached our desired rate yet.

The main point of Bloom filters is to be able to filter fast, and reliable (most of the time), so two things must come to mind before implementing a filter, which is the number of elements we want it to contain, and false positive rate tolerable.

Are there any known techniques or strategies to reduce the false positive rate in a Bloom filter?

Generally, the simple technique is just to increase $m$ to a very large number, approaching infinity while $n$ being finitely small, and $k$ is substantially less than $m$ . Taking the limit as $m\to \infty$ on the false positive rate equation, we can notice that $\epsilon \to 0$ .

Although, there has been a paper published that has done some research on constructing a false positive free zone for general filters. For a small number of $d$ , for a restrictedly finite universe of $U={1,...,n_d}$ then until at most $d$ elements are in the filter, it’s guaranteed that there will be no false positives for queries of elements from $U$ .

To put it simply, here’s the lemma: the filter has a false positive free zone with at most $d$ elements in the filter for universe $U={1,...,n_d=n}$ if:

n \leq \sqrt[d]{\prod_{j=1}^{k}p_j}

where $n$ is the threshold, and $p_j$ is the $j$ -th prime number such that ( $p_1=2$ , $p_2=3$ ,…), and $d$ being the level of the universe.

Is it possible to estimate the number of elements stored in a Bloom filter?

Yes, to an extent. The limitation is similar to the analogy that, with a ball on the top of a hill, given the gravitational force and the force applied to the ball, it is relatively simple to work out where the ball would land after rolling down, but given the destination and the force applied to the ball, it is nearly impossible to figure out where it started originally, as there are too many “points” in space to consider, but we can “guess” with a chance where it started. The same applies to Bloom filters, Swamidass & Baldi, showed that the number of items in a Bloom filter can be approximated with:

n^*= -\frac{m}{k}\ln\left(1-\frac{x}{m}\right)

where $n^*$ is the estimate of the number of items inserted, $m$ is the length of the bitset, $k$ being the number of hashers and $x$ being the number of bits that are “on”, or set to one.

Can a Bloom filter handle deletions of elements from the set it represents?

A simple Bloom filter can not per say, handle deletions of elements properly. If by deleting, we mean just changing one bit of the mapped indices to $0$ , which would already effectively remove that element from the set, but we don’t know if there are other elements that also by chance, map to a set of bits that consist of that bit. With a simple algorithm, we also have no way to know which bit to clear, as there are commonly multiple hash functions.

A more advanced variation of Bloom filter, a Counting Bloom Filter, where numbers are used to count, similarly to Counting Sort, instead of just a boolean value of true or false. A deletion is then possible, if and only if, that element has been added to the filter, and the number of times it was added is exactly once.

Can a Bloom filter be dynamically resized to accommodate more elements?

A Bloom filter works only when you know the number of elements to be inserted in advance, along with the desired false positive rate. A Bloom filter, technically, already can accommodate an infinite number of elements, but then, the false positive rate trends towards 1, which kind of already defeats the point of the filter.

If the threshold of “optimal elements count” is exceeded, a new Bloom filter with a larger capacity can be created if and only if we know exactly which elements that have been added, not just the bits that have been flipped, as moving from $m$ to $m'$ , the hash functions would yield different outputs. However, a Bloom filter only stores the probability of existence of any element, the elements themselves have to be stored externally, so for simple filters without that external storage, a dynamic resize is impossible.

Straying from the subject, there have been research on Scalable Bloom Filter, which itself is comprised of multiple small filters, and it allows an arbitrary growth of the set. Each successive filter is created with a tighter maximum error probability on a geometric progression, so that the compounded probability over the whole series converges, even given as the number tends towards infinity. Querying is then made by testing for presence in each filter.

Compare between Bloom Filter and Hash Table

Assuming, for bloom filters, we only care about the actual bit arrays, or integer arrays in the case of counting variation, and the actual elements do not get stored.

Feature	Bloom Filter	Hash Table	Counting Bloom Filter
Space Efficiency	$1.44\log_2(1/\epsilon)$ bits per key	However many bits a key needs	$1.44\log_2(1/\epsilon)$ integers per key
Time Efficiency	Always $O(k)$	The bigger the capacity, the closer to $O(1)$	Always $O(k)$
Insertion	Always $O(k)$	Depends on $O(h)$ where $h$ is the complexity of the hash function	Always $O(k)$
Deletion	Not possible	Depends on $O(h)$ again	Always $O(k)$ , provided that it exists
Queries	Always $O(k)$ , with a chance of false positives	Depends on $O(h)$ , no chance of false results	Always $O(k)$ , with a chance of false positives
Limitations	Can not be resized, can not know exact number of elements, false positives always exist	Much larger space size needed	Can not be resized, can not know exact count, false positives always exist

The integers that a counting filter uses usually only consist of $3$ to $4$ bits, so the space needed for them usually is about as three times or four times a simple filter.

With sufficient memory, a hash table is usually preferable, but with limited memory compared to how large the data is, a Bloom filter is used to minimize the number of reads needed, as false positives are possible but false negatives are not. So if an element doesn’t exist already, there’s no need to actually read anything to check.

Overall on Data Structures

The project is quite small and intuitive, where the sources folder would consist of 3 notable files:

main.cpp: Holding the actual main function, and where everything starts.
header.h: Where data structures and functions are declared.
func.cpp: The implementations of said structures and functions, to be called by main.

We are utilizing a few C++ libraries to help with the project:

iostream: Necessary to do standard input-output.
vector: An arbitrarily scalable array, used to hold the data.
bitset: A bit array, provided by the standard library.
fstream: Necessary to do standard files input-output.
string: An abstracted char array to make dealing with text easier.

We declare a simple Account to contain a username field and password field, both of type string. Another Database struct would hold a vector of Accounts. Then, the jam and butter, the struct BloomFilter would hold a bitset of arbitrarily large number of bits.

For the bloom filters, we chose $m=10,000,000$ (or ten million) bits to store and $k=50$ (or fifty) hash functions. Although we expect about $15000$ elements to be inserted, the dudes that worked on the coding part deliberately chose an absurdly high $m$ that the false positive rate is now approximately $9 \times 10^{-58}$ .

To grasp that number, our world today has about 8 billion people. If we pick 1 person at random, and it happens to be Tom Holland. Then do it again, and it again, happens to be Tom Holland. Then, again, again, again… In this imaginary scenario, if we do this random picking 5 times, and every single time it just happens to be Tom Holland, the probability of this happening is still $100,000,000\times$ more likely than a false positive turning up.

Program’s Lifecycle

A flowchart for easier grasping:

flowchart TD
   s1("Initializing")
   s2("Pull from local database (AccountFile.txt)")
   s1 --> s2
   s2 --> s3("Open menu for user")
   s3 --> c1{"If choice"}
   c1 --> |Exit| aExit("End program")
   c1 --> |No| aThing("Do the action")
   aThing --> s3